1
2
3
4
5
6
7
8
9
10
11
|
1
2
3
4
5
6
7
8
9
10
11
|
Seiten-Übersicht |
Auch die Eulerstäbe sollen nun auf ihre Stabilität untersucht werden. Gesucht wird wieder die Knicklast des Stabes, also die kleinste Last unter der sich der gebogene Stab im Gleichgewicht befindet. Der Stab ist dann in einer indifferenten Gleichgewichtslage und hat seine Stabilitätsgrenze erreicht. Das bereits beschriebene Vorgehen, nämlich das Aufstellen der Gleichgewichtsbedingungen am verformten System, kommt auch hier wieder zur Anwendung, da es allgemeingültig zur Untersuchung von Stabilitätsproblemen ist.
Wie man vorgeht um eine Eulersche Knicklast zu ermitteln, soll hier am Beispiel des Eulerstabs 2 erläutert werden. Es handelt sich dabei um einen beiderseits gelenkig gelagerten Stab, der durch eine Druckkraft F mittig belastet wird.
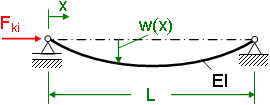Das Bild zeigt den Stab in einer verformten Lage
unter der kritischen Knicklast. Der Stab befindet sich im Gleichgewicht, über die Gleichgewichtsbedingungen kann jetzt die Knicklast bestimmt werden.
w(x) ist die Funktion der Biegelinie über den Stabverlauf. Die Längenänderung des Stabes aufgrund der Verformung darf
vernachlässigt werden. Bildet man Momentengleichgewicht um das linke Auflager, erkennt man, dass keine vertikalen Lagerkräfte auftreten.
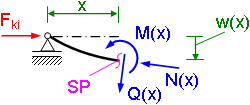Um etwas über die Größe der Knicklast zu erfahren, schneiden wir das verformte System an der Stelle x (siehe unteres Bild) und
stellen dieses Mal das Momentengleichgewicht um den Schnittpunkt SP auf. Dabei darf man beim Antragen der Kräfte die Schnittgrößen
im Stab nicht vergessen.
ΣM = 0: Fki · w (x) - M(x) = 0 ⇒ M(x) = Fki · w(x)
Aus der technischen Balkenbiegelehre ist der Zusammenhang zwischen Biegelinien- und Momentenfunktion bekannt.
Es gilt:
EI · w''(x) = - M(x)
Setzt man diesen Ausdruck in das Momentengleichgewicht ein, erhält man:
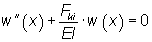
Um diese Differentialgleichung besser lösen zu können, wird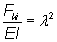
eingesetzt.
⇒ w''(x) + λ2 · w(x) = 0
Diese homogene DGL zweiter Ordnung mit konstanten Koeffizienten hat die allgemeine Lösung:
w(x) = A · sin(λ · x) + B · cos(λ · x)
Die Richtigkeit dieser Lösung kann man durch Einsetzten in die DGL leicht überprüfen. Die Konstanten
A und B werden über die Randbedingungen
bestimmt. An beiden Auflagern ist die Verschiebung
w = 0:
1. w(0) =0
⇒B = 0
2. w(L) =0
⇒A · sin(λ · L) = 0
Die 2. Randbedingung hat zum einen die triviale Lösung A = 0, die aber nicht interessiert, da sie die Gesamtlösung w(x) = 0 liefert, was der geraden Balkenachse entspricht. Es wird aber die Lösung gesucht, bei der der Stab jede beliebige gekrümmte Lage annehmen kann. Wenn A ≠ 0 ist, ist die Stabachse gekrümmt und es muss gelten: sin(λL) = 0 → λ · L = 0 ; π; 2π; 3π...
Bedenkt man, dass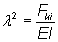 
, muss man die Lösung
(λ · L) = 0
ausschließen, da dann Fki ebenfalls verschwinden würde.
Interessant ist nur die kleinste von Null verschiedene Lösung, da sich der Stab unter der Last, die sich daraus ergibt, erstmals
gekrümmt im Gleichgewicht befindet. Die kritische Knicklast ergibt sich demnach aus
(λ · L) = π
zu:
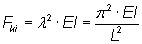
Beim Überschreiten dieser Druckkraft wird der Stab plötzlich ausknicken.
Die Funktion der Biegelinie für den ausgeknickten Stab lautet dann:
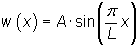
Für die Biegelinie ergibt sich die Form einer Sinusfunktion. Die maximale Auslenkung ergibt sich aus der Integrationskonstante B und bleibt unbestimmt, was ja für den indifferenten Gleichgewichtszustand typisch ist.
Als weiteres Beispiel gibt es hier
noch die Herleitung der Knicklast des Eulerstabs 4.
| Zwischenfrage: | |
|---|---|
|
Ein elastischer Stab mit konstanter Biegesteifigkeit EI ist oben eingespannt und am unteren Ende ebenfalls unverdrehbar aber
seitenverschieblich gelagert. Er ist durch eine Druckkraft mittig belastet.Wie sieht die zugehörige Knickform des Stabes aus? Klicken sie die richtige Antwort an. 
|
| Empfehlung: Falls Sie die Frage falsch beantwortet haben sollten lesen Sie nochmals die Seite 9. | |
